Pythagore et son Théorème : Une Aventure Mathématique
Qui était Pythagore ?
Pythagore était un philosophe et mathématicien grec né vers 570 av. J.-C. sur l’île de Samos. Il a voyagé en Égypte et en Mésopotamie, où il a acquis des connaissances en mathématiques et en astronomie. À son retour, il a fondé une école à Crotone, en Italie, connue sous le nom d’École pythagoricienne. Les membres de cette école suivaient un mode de vie communautaire et croyaient en la réincarnation et en la purification de l’âme.

Illustration représentant Pythagore et ses élèves

Illustration des premiers écrits de Pythagore
Les Contributions de Pythagore
Pythagore est surtout connu pour ses contributions aux mathématiques, mais il a également influencé la musique et la philosophie. Il a découvert que les intervalles musicaux pouvaient être exprimés en termes de rapports numériques simples, ce qui a conduit à la théorie des harmoniques. En philosophie, il a introduit l’idée que les nombres sont au cœur de l’univers et que tout peut être expliqué par les mathématiques.
Le Théorème de Pythagore
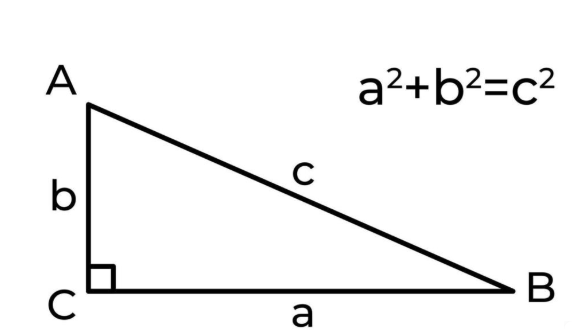
Le théorème de Pythagore est l’une des découvertes les plus célèbres de Pythagore. Il concerne les triangles rectangles, c’est-à-dire les triangles qui ont un angle droit (90 degrés). Le théorème énonce que dans un triangle rectangle, le carré de la longueur de l’hypoténuse (le côté opposé à l’angle droit) est égal à la somme des carrés des longueurs des deux autres côtés. En termes mathématiques, cela se formule ainsi :
a2 + b2 = c2
où (c) est l’hypoténuse et (a) et (b) sont les deux autres côtés.
Une Petite Histoire pour Illustrer
Imaginez que vous êtes un architecte dans la Grèce antique. Vous devez construire un temple avec un toit parfaitement droit. Pour vous assurer que les angles sont corrects, vous utilisez une corde avec des nœuds à intervalles réguliers pour former un triangle rectangle. Grâce au théorème de Pythagore, vous pouvez vérifier que votre triangle est bien rectangle en mesurant les côtés et en vérifiant que (a2 + b2 = c2 ).
Preuves du Théorème de Pythagore
Il existe de nombreuses preuves du théorème de Pythagore, certaines géométriques et d’autres algébriques. Une preuve géométrique classique consiste à dessiner un carré avec un triangle rectangle à chaque coin. En réarrangeant ces triangles, on peut montrer que les aires des carrés construits sur les deux côtés plus courts sont égales à l’aire du carré construit sur l’hypoténuse.
Applications Pratiques
Le théorème de Pythagore n’est pas seulement une curiosité mathématique ; il a de nombreuses applications pratiques. Par exemple, il est utilisé en architecture pour s’assurer que les angles sont droits, en ingénierie pour calculer des distances et des forces, en navigation pour déterminer des trajectoires, et même en informatique pour des calculs de distances dans des espaces multidimensionnels.
Un Petit Jeu
Pour rendre les choses plus amusantes, essayez de trouver des objets autour de vous qui forment des triangles rectangles. Mesurez les côtés et voyez si le théorème de Pythagore s’applique. Vous serez surpris de voir combien de fois ce théorème apparaît dans la vie quotidienne !
Conclusion
Le théorème de Pythagore est une découverte fondamentale qui a des implications profondes dans de nombreux domaines. Il illustre la beauté et l’universalité des mathématiques. En comprenant ce théorème, nous pouvons mieux apprécier les contributions de Pythagore et l’importance des mathématiques dans notre monde.
